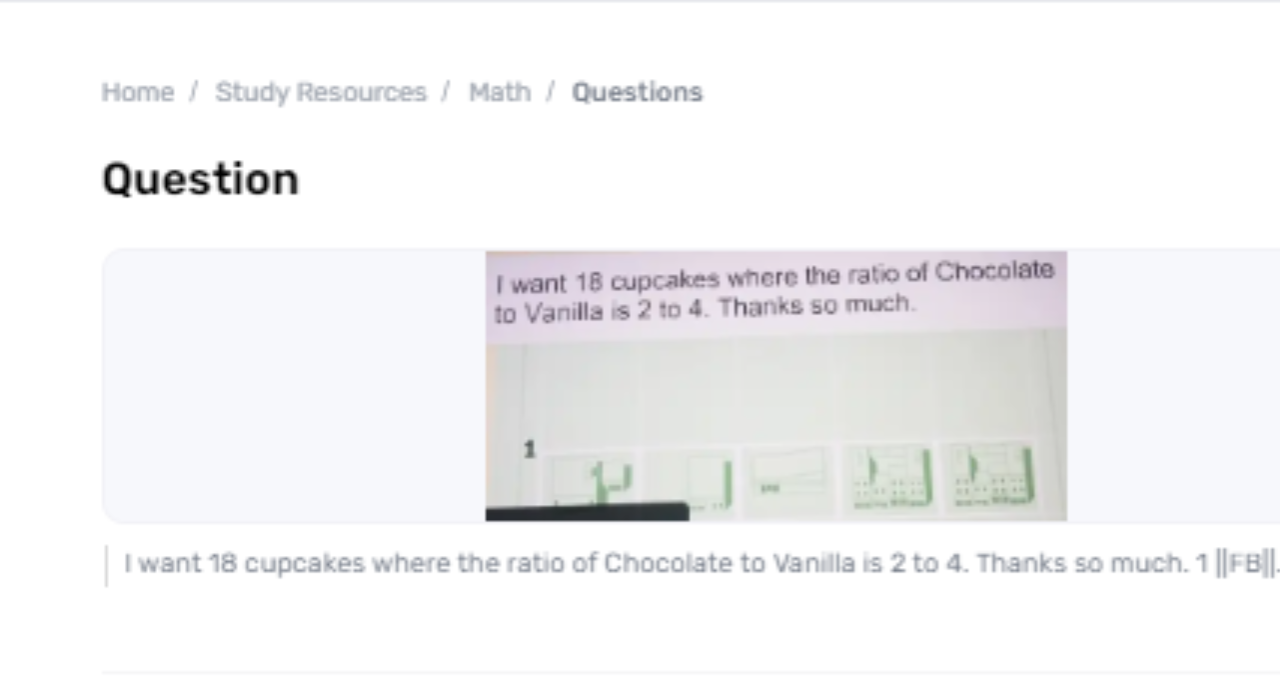
Proportions are a crucial concept in science utilized to compare amounts and illuminate issues including corresponding connections. When given a particular proportion and an add-up amount, it is frequently fundamental to decide the person's sums that fit the proportion. In this situation, the assignment is to partition 18 cupcakes into bunches taking after a proportion of 2 to 4. Understanding how to unravel such issues includes applying proportion concepts and essential number juggling operations. This exposition will investigate the method of deciding that if i want 18 cupcakes where the ratio is 2 to 4 the number of cupcakes in each gather when the proportion is 2 to 4 and the overall number is 18, giving a step-by-step arrangement and examining the implications of the result.
Understanding Proportions
A proportion could be a way to specify the relative measure of two amounts. It is composed as "a to b" or {a}{b}ba, where a and b speak to the amounts being compared. In this issue, the proportion is 2 to 4. This implies that for every 2 units of one amount, there are 4 units of another. Proportions can be rearranged or scaled to fit distinctive add up to sums. The key to fathoming proportion issues is understanding that the parts of the proportion must sum up to the entire amount when increased by the fitting calculation..
Calculating the Estimate of Each Portion
With the whole proportion parts known, the following step is to calculate the estimate of each portion. To do this, partition the full number of cupcakes by the full number of parts. In this case, we have 18 cupcakes and 6 add up to parts: Estimate of each part=186=3 {Size of each portion} = {18}{6} = 3 Estimate of each part=618=3 This calculation shows that each portion is comparable to 3 cupcakes. Therefore, each unit of the proportion compares to 3 cupcakes.
Deciding the Number of Cupcakes per Bunch
Having calculated the estimate of each portion, able to presently decide the number of cupcakes in each bunch agreeing to the proportion 2 to 4. For the primary bunch (which is spoken to by the 2 within the proportion), the number of cupcakes is: 2 parts3 cupcakes per part=6 For the moment gather (spoken to by the 4 within the proportion), the number of cupcakes is: 4 parts 3 cupcakes per part=12 Hence, within the proportion 2 to 4, the primary gather contains 6 cupcakes, and the moment gather contains 12 cupcakes.
Confirming the Arrangement
To guarantee that the arrangement is rectified, it is important to confirm that the whole number of cupcakes matches the given sum. Including the number of cupcakes in each group:
6 cupcakes+12 cupcakes=18 cupcakes The overall match the initial number of cupcakes, affirming that the calculation is adjusted. This confirmation step guarantees that the division of cupcakes agreeing to the given proportion is precise and total.
Steps for Tending to a Gauth Query
1. Determine the Question
Scope: Distinguish whether the inquiry is around setup, functionality, organization, or investigating to direct your reaction.
2. Retrieve Relevant Data:
Check Gauth’s official bolster assets and consider normal client issues to create a total reply.
3. Organize Your Reply: Show the data in a clear, precise arrangement, enumerating each step required to address the address.
4. Verify and Clean:
Guarantee the precision of the points of interest and refine the reaction for clarity and conciseness, making it open and simple to take after.
Conclusion
In conclusion, isolating 18 cupcakes into bunches with a proportion of 2 to 4 involves understanding the concept of ratios and applying essential math operations. By deciphering the proportion, calculating the estimate of each portion, and deciding the number of cupcakes in each bunch, we discover that the primary gather contains 6 cupcakes and the moment gather contains 12 cupcakes. This preparation not as it were outlines the viable application of proportions but moreover highlights the importance of confirming what comes about to guarantee precision. Mastery of such issues upgrades problem-solving aptitudes and develops an understanding of corresponding connections in science.